V-CLASS - SISTEM PENUNJANG KEPUTUSAN (SPEAK)
JULIUS FERNANDO/11108093/3KA06
Seorang pemborong akan membuat
dua macam tiang yang terbuat dari bahan beton. Tiang I memerlukan campuran 2
sak semen dan 3 karung pasir, sedangkan tiang II memerlukan campuran 1.5 sak
semen dan 2 karung pasir. Pemborong tersebut memiliki persediaan 15 sak semen
dan 21.5 karung pasir. Formulasikan dan selesaikan masalah ini !
Jawab:
Bahan (beton)
|
Tiang 1
|
Tiang 2
|
Persediaan
|
Semen (sack)
|
2
|
1.5
|
15
|
Pasir (kantung)
|
3
|
2
|
21.5
|
X1 = TIANG 1
X2 = TIANG 2
Persamaan linier yang didapat :
2X1 + 1.5X2 = 15
3X1 + 2X2 = 21.5
Pemecahan masalah :
ü Mencari nilai X2 (eliminasi X1)
2X1 + 1.5X2 = 15 | x 3 | 6X1
+ 4.5X2 = 45
0.5X2
= 2
X2 = 2/0.5 = 4
ü Mencari X1 (subtitusi nilai X2)
3X1 + 2X2 = 21.5 è 3X1 + 2(4) = 21.5
3X1
+ 8 = 21.5
3X1
= 21.5 – 8 =13.5
X1 = 13.5/3 = 4.5
Dari
perhitungan di atas, dapat kita definisikan nilai X1 = 4.5 dan nilai X2 = 4
Jika
kita melihat dalam tabel di atas maka akan dapat kita tarik kesimpulan :
ü Tiang 1 : Menghabiskan 2(4.5) = 9 sack semen; dan 3(4.5)
= 13.5 kantung pasir
ü Tiang 2 : Menghabiskan 1.5(4) = 6 sack semen; dan 2(4) =
8 kantung pasir
Total
keseluruhan penggunaan sack semen untuk tiang 1 dan tiang 2 yaitu :
9 + 6 = 15 (sack semen)
Total
keseluruhan penggunaan kantung pasir untuk tiang 1 dan tiang 2 yaitu :
13.5 + 8 = 21.5 (kantung pasir)
Perealisasian perhitungan dengan Ms.Excel
Langkah
pertama untuk pembuatan perhitungan X1 dan X2 pada ms.excel yaitu pembuatan
tabel awal terlebih dahulu.
Kemudian
buat tabel terpisah untuk nilai X1 dan X2. Masukkan formula perhitungan untuk
X1 terlebih dahulu dengan formula perhitungan eliminasi. Formula untuk
perhitungan eliminasi adalah : (D2-(C2*4))/B2
Setelah
selesai menghitung nilai X1, kemudian tentukan perhitungan X2 dengan
menggunakan formula untuk metode perhitungan subtitusi :
((D2*3)-(D3*2))/((C2*3)-(C3*2))
Setelah
nilai X1 dan X2 sudah ditentukan, selanjutnya buat tabel kesimpulan untuk
mengetahui jumlah total penggunaan bahan-bahan untuk pembuatan tiang 1 dan
tiang 2 (X1 dan X2) secara terpisah agar dapat dimengerti dengan mudah.
Kemudian
kerjakan formula satu-per-satu mulai dari penggunaan semen pada bahan tiang 1
(X1). Formula yang di isi cukup dengan mengalikan nilai bahan semen yg telah di isi pada tiang 1 (B2) dengan nilai X1 pada
tabel sebelumnya (A8).
Begitu
pula dengan perhitungan penggunaan kantung
pasir pada tiang 1 (X1).
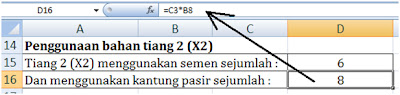
Untuk
tabel penggunaan keseluruhan bahan semen dan pasir pada tiang 2 (X2),
perhitungan yang di pakai hamper sama dengan perhitungan pada penggunaan bahan
tiang 1 (X1). Hanya saja berbeda pada kolom yang akan dihitung pada formulanya.
Lihat gambar di bawah.
Lalu
pada jumlah kantung pasir, pengisian formulanya hanya berbeda pada kolom C2
diganti menjadi C3, karena kolom C3 adalah nilai tetap jumlah kantung pasir
(lihat tabel pertama)